OLS、リッジ回帰、ラッソでのパフォーマンス比較
OLS、特徴選択、リッジ回帰、ラッソの4つの方法でTrainデータからモデルをFittingし、Testデータを用いて、平均2乗誤差(MSE)を推定して比べるといったことをします。
まずはデータの準備
データはStanford大学の統計学部からprostateのデータをダウンロード、正規化、訓練データ、テストデータに分けて使います。
> # Download prostate data > con = "http://statweb.stanford.edu/~tibs/ElemStatLearn/datasets/prostate.data" > prostate=read.csv(con,row.names=1,sep="\t") > > # Scale data and prepare train/test split > prost.std <- data.frame(cbind(scale(prostate[,1:8]),prostate$lpsa)) > names(prost.std)[9] <- 'lpsa' > data.train <- prost.std[prostate$train,] > data.test <- prost.std[!prostate$train,] > y.test <- data.test$lpsa > n.train <- nrow(data.train)
OLS
単純な最小二乗法でMSEを求めてみます。
> m.ols <- lm(lpsa ~ . , data=data.train) > summary(m.ols) Call: lm(formula = lpsa ~ ., data = data.train) Residuals: Min 1Q Median 3Q Max -1.64870 -0.34147 -0.05424 0.44941 1.48675 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 2.46493 0.08931 27.598 < 2e-16 *** lcavol 0.67953 0.12663 5.366 1.47e-06 *** lweight 0.26305 0.09563 2.751 0.00792 ** age -0.14146 0.10134 -1.396 0.16806 lbph 0.21015 0.10222 2.056 0.04431 * svi 0.30520 0.12360 2.469 0.01651 * lcp -0.28849 0.15453 -1.867 0.06697 . gleason -0.02131 0.14525 -0.147 0.88389 pgg45 0.26696 0.15361 1.738 0.08755 . --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.7123 on 58 degrees of freedom Multiple R-squared: 0.6944, Adjusted R-squared: 0.6522 F-statistic: 16.47 on 8 and 58 DF, p-value: 2.042e-12 > y.pred.ols <- predict(m.ols,data.test) > summary((y.pred.ols - y.test)^2) Min. 1st Qu. Median Mean 3rd Qu. Max. 0.000209 0.044030 0.116400 0.521300 0.445000 4.097000 > > mse.ols=sum((y.pred.ols - y.test)^2) > mse.ols [1] 15.63822
特徴選択
次に特徴量を減らしてみます。
leap関数でCp(Process Capability Index)をもとに特徴選択を行った上で、MSEを求めます。
whichで確認すると、gleasonを削ったモデルが良さそうだと判断されてます。
> library(leaps) > l <- leaps(data.train[,1:8],data.train[,9],method='Cp') > plot(l$size,l$Cp) > > # Select best model according to Cp > bestfeat <- l$which[which.min(l$Cp),] > bestfeat 1 2 3 4 5 6 7 8 TRUE TRUE TRUE TRUE TRUE TRUE FALSE TRUE > > # Train and test the model on the best subset > m.bestsubset <- lm(lpsa ~ .,data=data.train[,bestfeat]) > summary(m.bestsubset) Call: lm(formula = lpsa ~ ., data = data.train[, bestfeat]) Residuals: Min 1Q Median 3Q Max -1.65425 -0.34471 -0.05615 0.44380 1.48952 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 2.46687 0.08760 28.161 < 2e-16 *** lcavol 0.67645 0.12384 5.462 9.88e-07 *** lweight 0.26528 0.09363 2.833 0.0063 ** age -0.14503 0.09757 -1.486 0.1425 lbph 0.20953 0.10128 2.069 0.0430 * svi 0.30709 0.12190 2.519 0.0145 * lcp -0.28722 0.15300 -1.877 0.0654 . pgg45 0.25228 0.11562 2.182 0.0331 * --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.7064 on 59 degrees of freedom Multiple R-squared: 0.6943, Adjusted R-squared: 0.658 F-statistic: 19.14 on 7 and 59 DF, p-value: 4.496e-13 > y.pred.bestsubset <- predict(m.bestsubset,data.test[,bestfeat]) > summary((y.pred.bestsubset - y.test)^2) Min. 1st Qu. Median Mean 3rd Qu. Max. 0.000575 0.038000 0.122400 0.516500 0.449300 4.002000 > > mse.bestsubset=sum((y.pred.bestsubset - y.test)^2) > mse.bestsubset [1] 15.4954
リッジ回帰
次にリッジ回帰でやってみます。
リッジ回帰とラッソについて、なんだっけという場合は下記がご参考。
tjo.hatenablog.com
で、さくっとやってみます。
> library(MASS) > m.ridge <- lm.ridge(lpsa ~ .,data=data.train, lambda = seq(0,20,0.1)) > plot(m.ridge) > > #by using the select function > select(m.ridge) modified HKB estimator is 3.355691 modified L-W estimator is 3.050708 smallest value of GCV at 4.9
下記のような図と共に、ベストなλは4.9だと選ばれました。
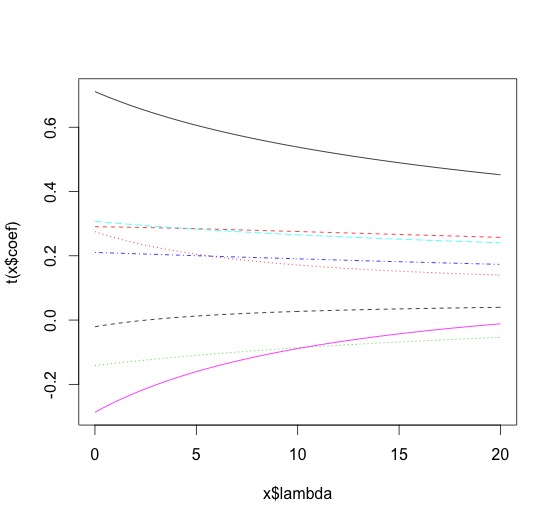
次に予測値を返させて、MSEを求めます。
> y.pred.ridge = scale(data.test[,1:8],center = m.ridge$xm, scale = m.ridge$scales)%*% m.ridge$coef[,which.min(m.ridge$GCV)] + m.ridge$ym > summary((y.pred.ridge - y.test)^2) V1 Min. :0.000003 1st Qu.:0.043863 Median :0.136450 Mean :0.494410 3rd Qu.:0.443495 Max. :3.809051 > mse.ridge=sum((y.pred.ridge - y.test)^2) > mse.ridge [1] 14.8323
ラッソ
あまり使っている見ませんが、larsライブラリー(https://cran.r-project.org/web/packages/lars/index.html)を使います。
> library(lars) > m.lasso <- lars(as.matrix(data.train[,1:8]),data.train$lpsa,type="lasso") > plot(m.lasso) > # Cross-validation > r <- cv.lars(as.matrix(data.train[,1:8]),data.train$lpsa) > bestfraction <- r$index[which.min(r$cv)] > bestfraction [1] 0.5252525
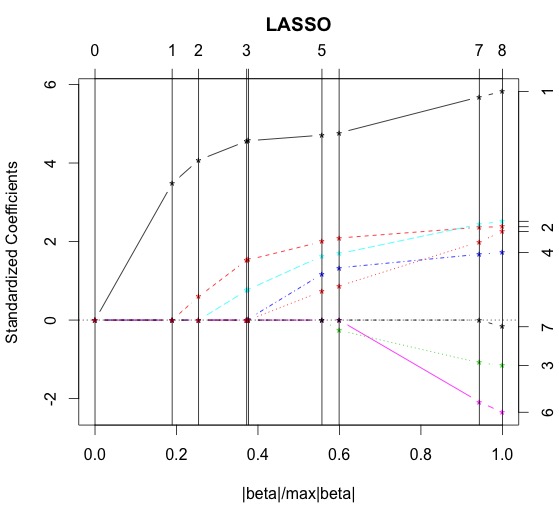
fractionは0.525あたりと図と出力から判断出来ます。
> # Observe coefficients > coef.lasso <- predict(m.lasso,as.matrix(data.test[,1:8]),s=bestfraction,type="coefficient",mode="fraction") > > # Prediction > y.pred.lasso <- predict(m.lasso,as.matrix(data.test[,1:8]),s=bestfraction,type="fit",mode="fraction")$fit > summary((y.pred.lasso - y.test)^2) Min. 1st Qu. Median Mean 3rd Qu. Max. 0.000144 0.072470 0.128000 0.454000 0.394400 3.565000 > > mse.lasso=sum((y.pred.lasso - y.test)^2) > mse.lasso [1] 13.61874 >
平均二乗誤差の比較
> # Compare them > mse.ols [1] 15.63822 > mse.bestsubset [1] 15.4954 > mse.ridge [1] 14.8323 > mse.lasso [1] 13.61874
今回のデータに関しては、ラッソで行った分析が一番MSEを最小に出来ました。