PRML 7章サポートベクトルマシン

パターン認識と機械学習、第7章「Sparse Kernel Machines」に入ってSVMの実装をしてみます。
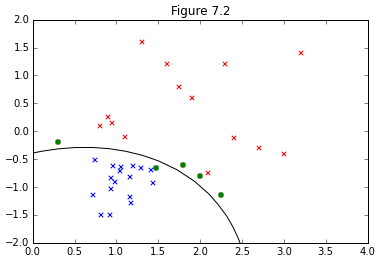
図7.2の再現を行うにあたり、カーネルがガウジアンカーネルが選択されているようなので、今回の実装もこれに従います。

いつも通り境界面の求め方など、SVMそのものの解説はPRMLやはじパタにお任せするとして、実装にあたっての流れだけ簡単に示します。

実装の大まかな流れ

①ラグランジュ関数の双対表現 (7.10)について、二次計画法で解く。

$\tilde{L}(a) = \sum_{n=1}^N a_n - \frac{1}{2} \sum_{n=1}^N \sum_{m=1}^N a_na_m t_n t_m k({\bf x_n}, {\bf x_m}) (7.10)$

非線形計画法の自前での実装はムリ！って言われたので、おとなしくソルバーを使いました。無償かつポピュラーっぽいcvxoptというライブラリーが良さ気なのでインストール。

f:id:tkzs:20150916005515p:plain

上記のようにドキュメントに従ってcvxoptでモデル化するには(7.10)のままだと見づらいので式変形。

$- \tilde{L}(a) = \frac{1}{2} {\bf A}^{\mathrm{T}} ({\bf T}^{\mathrm{T}} k({\bf x_n}, {\bf x_m}) {\bf T}){\bf A} - {\bf A} (7.10)'$

表記的には気持ち悪い形ですが、ひとまず(7.10)'とcvxoptを見比べながらモデル化できたらそのままcvxoptに解いてもらうとラグランジュ乗数 $a$ が求まります。

②SVMでは境界面の決定にサポートベクトルのみ関与し、これはKKT条件で絞り込まれます。
なんとなくまだ腹落ちしてないところもありますが、境界面上にあるベクトルは $t_ny({\bf x})-1=0$ になるので、(7.16)より、 $a>0$ でないといけないと解釈。これを利用してサポートベクトルを抽出します。

③で、求まったサポートベクトルを使って(7.18)の $b$ を求めます。

④(7.13)に求めた値を代入して、境界面を求めます。

コード

今回、図を描くのにえらい苦労しまいた。どうしても境界面が上手くプロットできず、aidiaryさんのこちらの記事を全面的に参考にさせて頂きました。ありがとうございました。

import math
import matplotlib.pyplot as plt
from scipy import stats
from scipy.stats.kde import gaussian_kde
from pylab import *
import numpy as np
import random
import cvxopt
from cvxopt import matrix, solvers
%matplotlib inline

def kernel(x, y):
    sigma = 5.0
    return np.exp(-norm(x-y)**2 / (2 * (sigma ** 2)))

#(7.10)' (Quadratic Programming)
def L(t, X, N):
    K = np.zeros((N, N))
    for i in range(N):
        for j in range(N):
            K[i, j] = t[i] * t[j] * kernel(X[i], X[j])
    Q = matrix(K)
    p = matrix(-1 * np.ones(N))             
    G = matrix(np.diag([-1.0]*N))       
    h = matrix(np.zeros(N))             
    A = matrix(t, (1,N))                
    b = matrix(0.0)                     
    sol = solvers.qp(Q, p, G, h, A, b)
    a = array(sol['x']).reshape(N)
    return a

#(7.13)
def y_x(a, t, X, N, b, x):
    sum = 0
    for n in range(N):
        sum += a[n] * t[n] * kernel(x, X[n])
    return sum + b

#(7.18)
def b(a, t, X, S):
    sum_A = 0
    for n in S:
        sum_B = 0
        for m in S:
            sum_B += a[m] * t[m] * kernel(X[n], X[m])
        sum_A += (t[n] - sum_B)
    return sum_A/len(S)

if __name__ == "__main__":
    N = 36
    mu_blue = [1,-1]
    cov = [[0.1,0.05], [0.05,0.1]]
    
    x_blue,y_blue = np.random.multivariate_normal(mu_blue, cov, N/2).T
    
    x_red = [0.3, 0.8, 0.9, 0.95, 1.1, 1.3, 1.6, 1.9, 1.75, 1.8, 2.0, 2.1, 2.3, 2.25, 2.4, 2.7, 3.0, 3.2]
    y_red = [-0.2, 0.1, 0.25, 0.14, -0.1, 1.6, 1.2, 0.6, 0.8, -0.6, -0.8, -0.75, 1.2, -1.15, -0.12, -0.3, -0.4, 1.4]
    
    t_blue = np.ones((1, N/2))
    t_red = -1*np.ones((1, N/2))

    blue = vstack((x_blue, y_blue))
    red = vstack((x_red, y_red))

    X = np.concatenate((blue, red), axis=1).T
    t = np.concatenate((t_blue, t_red), axis=1).T
    
    #(7.10)' (Quadratic Programming)
    a = L(t, X, N)

    #Extract Index of support vectors from (7.14) 
    S = []
    for n in range(len(a)):
        if a[n] < 0.0001: continue
        S.append(n)

    #(7.18)
    b = b(a, t, X, S)

    
    #Plot train data sets
    plt.scatter(x_blue,y_blue,color='b',marker='x')
    plt.scatter(x_red,y_red,color='r',marker='x')
    
    # Enphasize suport vectors
    for n in S:
        plt.scatter(X[n,0], X[n,1], color='g', marker='o')
    
    # Plot the decision surface
    X1, X2 = meshgrid(linspace(-10,10,100), linspace(-10,10,100))
    w, h = X1.shape
    X1.resize(X1.size)
    X2.resize(X2.size)
    Z = array([y_x(a, t, X, N, b, array([x1,x2])) for (x1, x2) in zip(X1, X2)])
    X1.resize((w, h))
    X2.resize((w, h))
    Z.resize((w, h))
    CS = contour(X1, X2, Z, [0.0], colors='k', linewidths=1, origin='lower')
    xlim(0, 4)
    ylim(-2, 2)
    title("Figure 7.2")

結果

f:id:tkzs:20150916011816p:plain

参考

非線形SVM - 人工知能に関する断創録