確率的勾配法あれこれまとめ
Kerasで選択できる最適化アルゴリズムそれぞれの違いと使い所がいまいちわからんかったので調べてみた。
Incorporating Nesterov Momentum into Adamがアルゴリズムを整理してくれているので理解しやすかった。
とりあえずざっくりと俯瞰した感じだと、いかに効率良く傾斜を降下していくかという課題を解決するっていう大枠からはみ出るものはない。そんで、構築しているモデルの種類やサイズによってベストなアルゴリズムは変わってくるので、突き詰めるのであれば要実験。ただ、上記論文は、NadamかRSMProp使っときゃいいんじゃないっすか、みたいなこと言ってる。なんにしろ2000年代後半以降で進化が進んでいる分野であり、今後もアップデートがあるだろうから追っていきたい。
SGD
まずはオーソドックスな勾配法。
後述するMomentum法や、NAGもKerasの中ではSGDメソッドの中でサポートされている。
Mpomentum
勾配に加えてMomentumベクトルを加えてパラメータを更新する。
Nesterov's accelerated gradient(NAG)
Momuentum法に対して、勾配計算の段階ですでにMomentumを考慮することで、現在のパラメータではなく、次のパラメーターの推定値について計算することで効率よく予測するアルゴリズム。
AdaGrad
それぞれ個別のパラメータに対して異なる学習率を適用するアルゴリズム。
学習率の補正にそれまでのパラメータ[\theta_i]の勾配の二乗和を用いるのでL2ノルムベースのアルゴリズムと分類される。
ここではさきのそれぞれのパラメータの勾配の二乗和のタイムステップ
までのベクトル
RSMProp
これもL2ノルムベース。前述の[n]に対して、勾配の二乗の減衰平均_t]を用いる。AdaGradで大きくなりすぎる[n]ことが問題だったがこれで解消。
Adam
Momentum法とRMSPropを組み合わせたもの。
勾配の1乗と勾配の2乗、両方使えばいいじゃん的な。
AdaMax
AdamのL2ノルムを拡張し無限にするとよりシンプルなアルゴリズムとなる、らしい。
Nadam
Adamと違ってNAGとRMSPropを組み合わせたもの。
参考

- 作者: 海野裕也,岡野原大輔,得居誠也,徳永拓之
- 出版社/メーカー: 講談社
- 発売日: 2015/04/08
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (5件) を見る
勾配降下法の 最適化アルゴリズム
CODE COMPLETE 第2版 を読んで
『CODE COMPLETE 第2版 上』、『CODE COMPLETE 第2版 下』を読み終えました。

CODE COMPLETE 第2版 上 完全なプログラミングを目指して
- 作者: スティーブマコネル,Steve McConnell,クイープ
- 出版社/メーカー: 日経BP社
- 発売日: 2005/03/26
- メディア: 単行本
- 購入: 44人 クリック: 1,166回
- この商品を含むブログ (288件) を見る

CODE COMPLETE 第2版 下 完全なプログラミングを目指して
- 作者: スティーブマコネル,Steve McConnell,クイープ
- 出版社/メーカー: 日経BP社
- 発売日: 2005/03/26
- メディア: 単行本
- 購入: 16人 クリック: 193回
- この商品を含むブログ (164件) を見る
正直、自分は大規模開発に携わったこともないし、もしかしたらこれから携わることもないかもしれない。そもそも、職業プログラマですらないかもしれない。けどプログラミングを道具として使う立場として、読んで理解できる部分は多かったです。
特に第7部の”ソフトウェア職人気質とは”では情報工学を学ばず、独学でやってきた自分がチームでプログラミングを行う際に注意すべきだろうなと思っていた、レイアウトやステートメントの仕方、変数の名付け方などが体型だって書いてあり、迷った際に帰ってくる部分ができたのがありがたかったです。
次の職務でどの程度コンストラクションに気をつけなければいけないかまだ検討が付かない段階ですので、他の多くの読者の方々とは得られたものが違ったかも知れません。
自分の業務の中でのプログラミングとの付き合い方がわかってくるであろう、半年後、一年後にもう一度読み直してみようと思います。
CodingBatでアルゴリズム100本ノック
これまでの自分のプログラミングは機械学習周辺に偏っていて、コンピューターサイエンスやったことある人間が通ってくる基本的なアルゴリズムについての知識が足りていないとの指摘を受けたので、その部分を埋めるためにCodingBatにチャレンジしてみた。
Coding Bat
http://codingbat.com/
簡単なアルゴリズムをひたすら書かせるプログラミングサイトで、初めの一歩として楽しくできた。
自分のコードはGitHubに載せておくことにする。
次はもう少し難しいアルゴリズムを練習するために、積読になっているこの本を練習する予定。

世界で闘うプログラミング力を鍛える150問 トップIT企業のプログラマになるための本
- 作者: Gayle Laakmann McDowell
- 出版社/メーカー: マイナビ出版
- 発売日: 2012/11/13
- メディア: Kindle版
- この商品を含むブログ (3件) を見る
Scikit-learnのpipeleine.Pipelineが便利
分析する際に、次元圧縮→分類のような流れで行う場合には、scikit-learnのPipelineが便利。特にハイパーパラメーターを探すときには手続が煩雑になることもありますが、まとめて分類器としててGridSearchCVに突っ込むだけで良いのでめんどくさいこと考えずに済みますね。
今回はScikit-learnのサンプルデータの中から、the digits datasetのデータをロードし、PCAでの次元圧縮からSVMでの分類をPipelineでまとめて実行する手順を確認してみました。
コード
まずはデータを読み込み、訓練データとテストデータに分割。
また手書き文字のデータがどんなものかを描き出します。
import numpy as np from sklearn import svm from sklearn.decomposition import PCA from sklearn import datasets from sklearn.grid_search import GridSearchCV from sklearn.pipeline import Pipeline from sklearn.cross_validation import train_test_split from sklearn import metrics from matplotlib import pyplot as plt from matplotlib import cm %matplotlib inline digits = datasets.load_digits() X = digits.data y = digits.target print 'Number of data = {0}, Dimension = {1}'.format(X.shape[0],X.shape[1]) p = np.random.random_integers(0, len(digits.data), 25) for index, (data, label) in enumerate(np.array(zip(digits.data, digits.target))[p]): plt.subplot(5, 5, index + 1) plt.axis('off') plt.imshow(data.reshape(8, 8), cmap=plt.cm.gray_r, interpolation='nearest') plt.title('%i' % label) plt.show() #Split the data X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2) Number of data = 1797, Dimension = 64

続いて、PCAで次元削減、SVMでの分類という2つの手順を一つのPipelineで分類器としてまとめます。
今回グリッドサーチでパラメータ探索するためにリスト形式で候補を入れてます。
複数の関数にまたがってパラメーターを指定することになるため、ハイフン二つの後にパラメーター名を指定することで、コントラクタに渡すようになってます。
estimators = [('pca', PCA()), ('svm', svm.SVC())] parameters = {"pca__n_components" : range(2, 6), "svm__kernel" : ["linear", "poly", "rbf", "sigmoid"], 'svm__C': np.logspace(0, 2, 10).tolist(), "svm__gamma": np.logspace(-3, 0, 10).tolist()} pl = Pipeline(estimators)
最後にplを一つの分類器としてみなし、そのままGridSearchCVに突っ込みます。
clf = GridSearchCV(pl, parameters, n_jobs=-1) clf.fit(X_train, y_train) print 'Best_estimator = {0}'.format(clf.best_estimator_.get_params()) #予測 Predict = clf.predict(X_test) n_samples = len(digits.data) expected = digits.target[n_samples * -4 / 10:] predicted = clf.predict(digits.data[n_samples * -4 / 10:]) print("Classification report for classifier %s:\n%s\n" % (clf, metrics.classification_report(expected, predicted))) print("Confusion matrix:\n%s" % metrics.confusion_matrix(expected, predicted)) Best_estimator = {'svm__max_iter': -1, 'svm__coef0': 0.0, 'svm': SVC(C=1.6681005372, cache_size=200, class_weight=None, coef0=0.0, decision_function_shape=None, degree=3, gamma=0.01, kernel='rbf', max_iter=-1, probability=False, random_state=None, shrinking=True, tol=0.001, verbose=False), 'svm__random_state': None, 'pca__copy': True, 'svm__degree': 3, 'pca__n_components': 5, 'svm__gamma': 0.01, 'svm__shrinking': True, 'pca__whiten': False, 'svm__tol': 0.001, 'svm__verbose': False, 'svm__C': 1.6681005372000588, 'steps': [('pca', PCA(copy=True, n_components=5, whiten=False)), ('svm', SVC(C=1.6681005372, cache_size=200, class_weight=None, coef0=0.0, decision_function_shape=None, degree=3, gamma=0.01, kernel='rbf', max_iter=-1, probability=False, random_state=None, shrinking=True, tol=0.001, verbose=False))], 'svm__probability': False, 'svm__class_weight': None, 'pca': PCA(copy=True, n_components=5, whiten=False), 'svm__decision_function_shape': None, 'svm__kernel': 'rbf', 'svm__cache_size': 200} Classification report for classifier GridSearchCV(cv=None, error_score='raise', estimator=Pipeline(steps=[('pca', PCA(copy=True, n_components=None, whiten=False)), ('svm', SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0, decision_function_shape=None, degree=3, gamma='auto', kernel='rbf', max_iter=-1, probability=False, random_state=None, shrinking=True, tol=0.001, verbose=False))]), fit_params={}, iid=True, n_jobs=-1, param_grid={'pca__n_components': [2, 3, 4, 5], 'svm__C': [1.0, 1.6681005372000588, 2.7825594022071245, 4.641588833612778, 7.742636826811269, 12.91549665014884, 21.544346900318832, 35.93813663804626, 59.94842503189409, 100.0], 'svm__gamma': [0.001, 0.0021544346900318843, 0.004641588833612777, 0.01, 0.021544346900318832, 0.046415888336127774, 0.1, 0.21544346900318823, 0.46415888336127775, 1.0]}, pre_dispatch='2*n_jobs', refit=True, scoring=None, verbose=0): precision recall f1-score support 0 1.00 0.96 0.98 71 1 0.99 0.97 0.98 73 2 0.94 0.93 0.94 71 3 0.95 0.96 0.95 74 4 0.96 0.96 0.96 74 5 0.97 1.00 0.99 71 6 0.99 1.00 0.99 74 7 0.93 0.92 0.92 72 8 0.84 0.85 0.85 68 9 0.90 0.92 0.91 71 avg / total 0.95 0.95 0.95 719 Confusion matrix: [[68 0 0 0 2 0 1 0 0 0] [ 0 71 0 0 0 0 0 1 0 1] [ 0 0 66 1 0 0 0 0 2 2] [ 0 0 0 71 0 0 0 2 0 1] [ 0 0 0 0 71 0 0 0 3 0] [ 0 0 0 0 0 71 0 0 0 0] [ 0 0 0 0 0 0 74 0 0 0] [ 0 1 0 0 0 0 0 66 5 0] [ 0 0 4 0 1 0 0 2 58 3] [ 0 0 0 3 0 2 0 0 1 65]]
Spark MLlibの協調フィルタリングを活用したMovie Recommendation
Sparkを触る機会が増えてきてるので、知識の棚卸しを兼ねてMLlib使ってレコメンデーションシステムを実装してみました。SparkSamit2014などMLlibのチュートリアル的に色々使われているSparkのMovie Recommendationですが、edXのIntroduction to Big Data with Apache Sparが内容的にも良さそうだったので、題材にしながら実装しました。本講座はSpark 1.3.1での実装ですが少し古すぎるので、1.6.1で使える機能は使う形でコード変えてます。
おおまかな手順
①データの準備
元データを訓練、評価、テストデータにそれぞれ分割
②評価数500以上の映画の中から平均評価点が高いものを表示
③協調フィルタリングの実装
④訓練データに自分をuserID"0"として加え、好きな映画を評価
⑤自分の評価をもとに、アルゴリズムに映画を推薦させる
コード
まずはデータを読み込んで分割、眺めてみます。
使うデータはUserID::MovieID::Rating::Timestampで構成されるmovieデータセットと、MovieID::Title::Genresで構成されるRatingデータセットがあります。
numPartitions = 2 ratingFileName = "ratings.txt" rawRatings = sc.textFile(ratingFileName, numPartitions) moviesFileName = "movies.txt" rawMovies = sc.textFile(moviesFileName, numPartitions) def get_ratings_tuple(entry): items = entry.split('::') return int(items[0]), int(items[1]), float(items[2]) def get_movie_tuple(entry): items = entry.split('::') return int(items[0]), items[1] ratingsRDD = rawRatings.map(get_ratings_tuple).cache() moviesRDD = rawMovies.map(get_movie_tuple).cache() ratingsCount = ratingsRDD.count() moviesCount = moviesRDD.count() print 'There are %s ratings and %s movies in the datasets' % (ratingsCount, moviesCount) print 'Ratings: %s' % ratingsRDD.take(3) print 'Movies: %s' % moviesRDD.take(3) There are 1000209 ratings and 3883 movies in the datasets Ratings: [(1, 1193, 5.0), (1, 661, 3.0), (1, 914, 3.0)] Movies: [(1, u'Toy Story (1995)'), (2, u'Jumanji (1995)'), (3, u'Grumpier Old Men (1995)')]
どのような映画が人気か調べるため500以上のReviewがある中で、人気の高いものを20個選び出します。
MovieIDと評価の数、平均評価点を含むRDDを作成し、それとmovieRDDをjoinさせることで、(平均評価点、映画のタイトル、評価数)を持つタプルを生成します。
その後、評価数が500個以上あるタイトルのみ選び出し、平均評価点でソートしたものを求めます。
評価点と映画のタイトルのアルファベット順でのソートのためにsortFunction()という関数を作ってます。
def getCountsAndAverages(IDandRatingsTuple): aggr_result = (IDandRatingsTuple[0], (len(IDandRatingsTuple[1]), float(sum(IDandRatingsTuple[1])) / len(IDandRatingsTuple[1]))) return aggr_result movieNameWithAvgRatingsRDD = (ratingsRDD .map(lambda x:(x[1], x[2])) .groupByKey() .map(getCountsAndAverages) .join(moviesRDD) .map(lambda x:(x[1][0][1], x[1][1], x[0]))) print 'movieNameWithAvgRatingsRDD: %s\n' % movieNameWithAvgRatingsRDD.take(3) def sortFunction(tuple): key = unicode('%.3f' % tuple[0]) value = tuple[1] return (key + ' ' + value) movieLimitedAndSortedByRatingRDD = (movieNameWithAvgRatingsRDD .filter(lambda x: (x[2] > 500)) .sortBy(sortFunction, False)) print 'Movies with highest ratings:' print '(average rating, movie name, number of reviews)' for ratingsTuple in movieLimitedAndSortedByRatingRDD.take(10): print ratingsTuple movieNameWithAvgRatingsRDD: [(3.49618320610687, u'Great Mouse Detective, The (1986)', 2048), (3.7871690427698574, u'Moonstruck (1987)', 3072), (2.7294117647058824, u'Waiting to Exhale (1995)', 4)] Movies with highest ratings: (average rating, movie name, number of reviews) (5.0, u'Ulysses (Ulisse) (1954)', 3172) (5.0, u'Song of Freedom (1936)', 3382) (5.0, u'Smashing Time (1967)', 3233) (5.0, u'Schlafes Bruder (Brother of Sleep) (1995)', 989) (5.0, u'One Little Indian (1973)', 3607) (5.0, u'Lured (1947)', 3656) (5.0, u'Gate of Heavenly Peace, The (1995)', 787) (5.0, u'Follow the Bitch (1998)', 1830) (5.0, u'Bittersweet Motel (2000)', 3881) (5.0, u'Baby, The (1973)', 3280)
次に協調フィルタリングを使用したレコメンデーションを実施します。
MLlibにはALSを使ったライブラリがあるのでそのまんま活用します。
ひとまずモデル構築のために訓練、評価、テストデータにデータセットを分割します。
trainingRDD, validationRDD, testRDD = ratingsRDD.randomSplit([6, 2, 2], seed=0) print 'Training: %s, validation: %s, test: %s\n' % (trainingRDD.count(), validationRDD.count(), testRDD.count()) print trainingRDD.take(3) print validationRDD.take(3) print testRDD.take(3) validationForPredictRDD = validationRDD.map(lambda x: (x[0], x[1])) print validationForPredictRDD.take(3) actualReformattedRDD = validationRDD.map(lambda x: ((x[0], x[1]), x[2])) print actualReformattedRDD.take(3) Training: 600364, validation: 199815, test: 200030 [(1, 661, 3.0), (1, 914, 3.0), (1, 1197, 3.0)] [(1, 3408, 4.0), (1, 2355, 5.0), (1, 938, 4.0)] [(1, 1193, 5.0), (1, 1287, 5.0), (1, 2804, 5.0)] [(1, 3408), (1, 2355), (1, 938)] [((1, 3408), 4.0), ((1, 2355), 5.0), ((1, 938), 4.0)]
モデル構築ですが、グリッドサーチによってより良いパラメーターを探します。
またモデルの評価にはMLlibに用意されている指標の中で平均二乗誤差の平方根(RMSE)を使います。
from pyspark.mllib.recommendation import ALS from pyspark.mllib.evaluation import RegressionMetrics seed = 5L iterations = [5,7,10] regularizationParameter = 0.1 ranks = [4, 8, 12] RMSEs = [0, 0, 0, 0, 0, 0, 0, 0, 0] err = 0 tolerance = 0.03 minRMSE = float('inf') bestRank = -1 bestIteration = -1 for rank in ranks: for iteration in iterations: model = ALS.train(trainingRDD, rank, seed=seed, iteration, lambda_=regularizationParameter) predictedRatingsRDD = model.predictAll(validationForPredictRDD) predictedReformattedRDD = predictedRatingsRDD.map(lambda x: ((x[0], x[1]), x[2])) predictionAndObservations = (predictedReformattedRDD .join(actualReformattedRDD) .map(lambda x: x[1])) metrics = RegressionMetrics(predictionAndObservations) RMSE = metrics.rootMeanSquaredError RMSEs[err] = RMSE err += 1 print 'For rank %s and itereation %s, the RMSE is %s' % (rank, iteration, RMSE) if RMSE < minRMSE: minRMSE = RMSE bestIteretioin = iteretaion bestRank = rank print 'The best model was trained with rank %s and iteratin %s' % (bestRank, bestIteretion) For rank 4 and itereation 5, the RMSE is 0.903719946201 For rank 4 and itereation 7, the RMSE is 0.893408395534 For rank 4 and itereation 10, the RMSE is 0.886260195446 For rank 8 and itereation 5, the RMSE is 0.89365207233 For rank 8 and itereation 7, the RMSE is 0.883901283207 For rank 8 and itereation 10, the RMSE is 0.876701840863 For rank 12 and itereation 5, the RMSE is 0.887127524585 For rank 12 and itereation 7, the RMSE is 0.87863327159 For rank 12 and itereation 10, the RMSE is 0.872532683651 The best model was trained with rank 12 and iteratin 10
テストデータでチェックします。RMSEに問題ないので過学習は起こしてなさそうです。
bestModel = ALS.train(trainingRDD,
bestRank,
seed=seed,
iterations=bestIteretion,
lambda_=regularizationParameter)
testForPredictingRDD = testRDD.map(lambda x: (x[0], x[1]))
testReformattedRDD = testRDD.map(lambda x: ((x[0], x[1]), x[2]))
predictedTestRDD = bestModel.predictAll(testForPredictingRDD)
predictedTestReformattedRDD = predictedTestRDD.map(lambda x: ((x[0], x[1]), x[2]))
predictionAndObservationsTest = (predictedTestReformattedRDD
.join(testReformattedRDD)
.map(lambda x: x[1]))
metrics = RegressionMetrics(predictionAndObservationsTest)
testRMSE = metrics.rootMeanSquaredError
print 'The model had a RMSE on the test set of %s' % testRMSE
The model had a RMSE on the test set of 0.87447554868
最後に自分の好きな映画を評価し、userID"0"としてデータに追加。その評価に基づいて映画を推薦してもらいます。
movieRDDから自分の好きな映画を取り出して評価して加え、モデルの訓練に使用します。その後、userID"0"向けの予測を得て、評価点の高いものから表示するようにします。
myUserID = 0 myRatedMovies = [(myUserID, 1, 5), #Toy Story (myUserID, 648, 3), # Mission Impossible (myUserID, 1580, 4), # Men In Black (myUserID, 1097, 3), # ET (myUserID, 3247, 5)] #Sister Act myRatingsRDD = sc.parallelize(myRatedMovies) trainingWithMyRatingsRDD = trainingRDD.union(myRatingsRDD) myRatingsModel = ALS.train(trainingWithMyRatingsRDD, bestRank, seed=seed, iterations=bestIteretion, lambda_=regularizationParameter) myUnratedMoviesRDD = (moviesRDD .filter(lambda x: x[0] not in [x[1] for x in myRatedMovies]) .map(lambda x: (myUserID, x[0]))) predictedRatingsRDD = myRatingsModel.predictAll(myUnratedMoviesRDD) predictedRDD = predictedRatingsRDD.map(lambda x: (x[1], x[2])) movieCountsRDD = (ratingsRDD .map(lambda x:(x[1], x[2])) .groupByKey() .map(getCountsAndAverages) .map(lambda x: (x[0], x[1][0]))) #Marge PredictedRDD and CountsRDD predictedWithCountsRDD = (predictedRDD .join(movieCountsRDD)) ratingsWithNamesRDD = (predictedWithCountsRDD .filter(lambda x: x[1][1] > 75) .join(moviesRDD) .map(lambda x: (x[1][0][0], x[1][1], x[1][0][1]))) predictedHighestRatedMovies = ratingsWithNamesRDD.takeOrdered(10, key=lambda x: -x[0]) print ('My highest rated movies as predicted (for movies with more than 75 reviews):\n%s' % '\n'.join(map(str, predictedHighestRatedMovies))) My highest rated movies as predicted (for movies with more than 75 reviews): (4.74482593848827, u'Sound of Music, The (1965)', 882) (4.580669496447569, u'Mary Poppins (1964)', 1011) (4.486424714752521, u'Beauty and the Beast (1991)', 1060) (4.478042748281928, u'Mulan (1998)', 490) (4.477453571213953, u'Toy Story 2 (1999)', 1585) (4.439390718632932, u'Fantasia 2000 (1999)', 453) (4.405894101045507, u'FairyTale: A True Story (1997)', 87) (4.4030583744108425, u"Singin' in the Rain (1952)", 751) (4.390333274084924, u'Top Hat (1935)', 251) (4.347757079374581, u'Gone with the Wind (1939)', 1156)
ベタな映画を評価してるので、ベタな映画が推薦されてますね笑
Spark MllibでのClick through rate(CRT) 予測
1年以上も前ですが、edXのScalable Machine learningを受講していた時のコードが出てきたので、見直してみました。この講座のネタが、KaggleのCriteoのコンペのデータ
を基にしたCTR予測でして、One-hot-encodingやhushingした高次元のデータを
Mllibのロジスティック回帰モデル
)で予測をするといったものです。今回は予測精度そのものよりも、ハッシュ関数で次元圧縮したものが、OHE化したデータと比べてどの程度予測精度に差が出るのかを見ていきます。
Sparkもかなり前のバージョンだったので、今ならまた違う実装の仕方があるような気もしますが、出来合いの機能に頼らずに実装したことで理解が深まった記憶があるので、そのまんま。追加機能の勉強兼ねた比較はまた別のタイミングで行いたいなと思います。 SparkはVirtualbox上にたてたUbuntuにインストールしたものをシングルノードで使用しています。
おおまかな手順
①データの準備
元データを訓練、評価、テストデータにそれぞれ分割
②元データにOHEを適用。ここで特徴量は20万以上になります。
③OHE後のデータでロジスティック回帰で分析(model1)
④ハッシュトリックで次元量の削減(およそ3,000程度)
⑤ハッシュ後のデータでロジスティック回帰分析
-Mllibデフォルト設定のモデル(model2)
-グリッドサーチでパラメータ設定したモデル(model3)
⑥Loglosによるモデル評価
-OHEデータモデル(model1) vs Hushingデータモデル(model2)
-Hushingデータ・デフォルトモデル(model2) vs Hushingデータ・GSモデル(model3)
コード
まずはデータを読み込んで分割、眺めてみます。
import numpy as np from pyspark.mllib.linalg import SparseVector from pyspark.mllib.regression import LabeledPoint rawData = (sc.textFile("dac_sample.txt").map(lambda x: x.replace('\t', ','))) OneSample = rawData.take(1) print OneSample weights = [.8, .1, .1] seed = 42 rawTrainData, rawValidationData, rawTestData = rawData.randomSplit(weights, seed) #Cache each datasets as it is used repeatedly rawTrainData.cache() rawValidationData.cache() rawTestData.cache() nTrain = rawTrainData.count() nVal = rawValidationData.count() nTest = rawTestData.count() print nTrain, nVal, nTest, nTrain + nVal + nTest [u'0,1,1,5,0,1382,4,15,2,181,1,2,,2,68fd1e64,80e26c9b,fb936136,7b4723c4,25c83c98,7e0ccccf,de7995b8,1f89b562,a73ee510,a8cd5504,b2cb9c98,37c9c164,2824a5f6,1adce6ef,8ba8b39a,891b62e7,e5ba7672,f54016b9,21ddcdc9,b1252a9d,07b5194c,,3a171ecb,c5c50484,e8b83407,9727dd16'] 79911 10075 10014 100000
OHEを分割したデータに当てます。
def createOneHotDict(inputData): OHEDict = (inputData .flatMap(lambda x: x) .distinct() .zipWithIndex() .collectAsMap()) return OHEDict def parsePoint(point): items = point.split(',') return [(i, item) for i, item in enumerate(items[1:])] def oneHotEncoding(rawFeats, OHEDict, numOHEFeats): sizeList = [OHEDict[f] for f in rawFeats if f in OHEDict] sortedSizeList = sorted(sizeList) valueList = [1 for f in rawFeats if f in OHEDict ] return SparseVector(numOHEFeats, sortedSizeList, valueList) def parseOHEPoint(point, OHEDict, numOHEFeats): parsedPoints = parsePoint(point) items = point.split(',') label = items[0] features = oneHotEncoding(parsedPoints, OHEDict, numOHEFeats) return LabeledPoint(label, features) parsedFeat = rawTrainData.map(parsePoint) ctrOHEDict = createOneHotDict(parsedFeat) numCtrOHEFeats = len(ctrOHEDict.keys()) OHETrainData = rawTrainData.map(lambda point: parseOHEPoint(point, ctrOHEDict, numCtrOHEFeats)).cache() OHEValidationData = rawValidationData.map(lambda point: parseOHEPoint(point, ctrOHEDict, numCtrOHEFeats)).cache() OHETestData = rawTestData.map(lambda point: parseOHEPoint(point, ctrOHEDict, numCtrOHEFeats)).cache() print ('Feature size after OHE:\n\tNumber of features = {0}' .format(numCtrOHEFeats)) print OHETrainData.take(1) Feature size after OHE: Number of features = 233286 [LabeledPoint(0.0, (233286,[386,3077,6799,8264,8862,11800,12802,16125,17551,18566,29331,33132,39525,55794,61786,81396,82659,93573,96929,100677,109699,110646,112132,120260,128596,132397,132803,140620,160675,185498,190370,191146,195925,202664,204273,206055,222737,225958,229942],[1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0]))]
OHE後のデータにてロジスティック回帰を実施。とりあえずパラメーター設定はデフォルトのままやってみます。
from pyspark.mllib.classification import LogisticRegressionWithSGD numIters = 100 stepSize = 1.0 regParam = 0.01 regType = 'l2' includeIntercept = True model0 = LogisticRegressionWithSGD.train(data = OHETrainData, iterations = numIters, step = stepSize, regParam = regParam, regType = regType, intercept = includeIntercept) #Compute loglos from math import log, exp def computeLogLoss(p, y): epsilon = 10e-12 if y == 1: return -log(epsilon + p) if p == 0 else -log(p) elif y == 0: return -log(1 - p + epsilon) if p == 1 else -log(1 - p) def getP(x, w, intercept): rawPrediction = x.dot(w) + intercept # Bound the raw prediction value rawPrediction = min(rawPrediction, 20) rawPrediction = max(rawPrediction, -20) return 1.0 / (1.0 + exp(-rawPrediction)) def evaluateResults(model, data): return data.map(lambda x: computeLogLoss(getP(x.features, model.weights, model.intercept), x.label)).sum() / data.count() logLossValLR0 = evaluateResults(model0, OHEValidationData) print ('Validation Logloss for model1:\n\t = {0}' .format(logLossValLR0))
素うどんのロジスティック回帰でどこまで予測できてるか、ROC曲線を描いてみます。ぼちぼちの精度でできてるようでした。
labelsAndScores = OHEValidationData.map(lambda lp: (lp.label, getP(lp.features, model0.weights, model0.intercept))) labelsAndWeights = labelsAndScores.collect() labelsAndWeights.sort(key=lambda (k, v): v, reverse=True) labelsByWeight = np.array([k for (k, v) in labelsAndWeights]) length = labelsByWeight.size truePositives = labelsByWeight.cumsum() numPositive = truePositives[-1] falsePositives = np.arange(1.0, length + 1, 1.) - truePositives truePositiveRate = truePositives / numPositive falsePositiveRate = falsePositives / (length - numPositive) import matplotlib.pyplot as plt %matplotlib inline fig = plt.figure() ax = plt.subplot(111) ax.set_xlim(-.05, 1.05), ax.set_ylim(-.05, 1.05) ax.set_ylabel('True Positive Rate (Sensitivity)') ax.set_xlabel('False Positive Rate (1 - Specificity)') plt.plot(falsePositiveRate, truePositiveRate, color='#8cbfd0', linestyle='-', linewidth=3.) plt.plot((0., 1.), (0., 1.), linestyle='--', color='#d6ebf2', linewidth=2.)
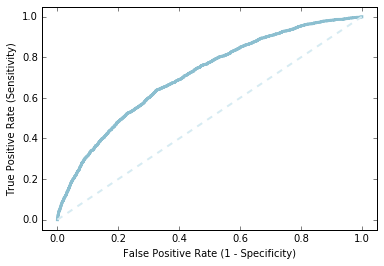
次に元データに対してハッシュトリックを当てます。
OHE後の次元数は20万程度、今回ハッシュ関数のバケット数を2の15乗で32768個としてます。
from collections import defaultdict import hashlib def hashFunction(numBuckets, rawFeats, printMapping=False): mapping = {} for ind, category in rawFeats: featureString = category + str(ind) mapping[featureString] = int(int(hashlib.md5(featureString).hexdigest(), 16) % numBuckets) sparseFeatures = defaultdict(float) for bucket in mapping.values(): sparseFeatures[bucket] += 1.0 return dict(sparseFeatures) def parseHashPoint(point, numBuckets): parsedPoints = parsePoint(point) items = point.split(',') label = items[0] features = hashFunction(numBuckets, parsedPoints, printMapping=False) return LabeledPoint(label, SparseVector(numBuckets, features)) numBucketsCTR = 2 ** 15 hashTrainData = rawTrainData.map(lambda x: parseHashPoint(x, numBucketsCTR)) hashTrainData.cache() hashValidationData = rawValidationData.map(lambda x: parseHashPoint(x, numBucketsCTR)) hashValidationData.cache() hashTestData = rawTestData.map(lambda x: parseHashPoint(x, numBucketsCTR)) hashTestData.cache() print ('Feature size after hushing:\n\tNumber of features = {0}' .format(numBucketsCTR)) print hashTrainData.take(1) Feature size after hushing: Number of features = 32768 [LabeledPoint(0.0, (32768,[1305,2883,3807,4814,4866,4913,6952,7117,9985,10316,11512,11722,12365,13893,14735,15816,16198,17761,19274,21604,22256,22563,22785,24855,25202,25533,25721,26487,26656,27668,28211,29152,29402,29873,30039,31484,32493,32708],[1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0]))]
ハッシュ関数をあてた後のデータにてロジスティック分析。
デフォルト設定のものと、グリッドサーチでパラメータを探したものと二つモデルを作ります。
まずは素うどんの方から。
numIters = 100 stepSize = 1.0 regParam = 0.01 regType = 'l2' includeIntercept = True model1 = LogisticRegressionWithSGD.train(data = hashTrainData, iterations = numIters, step = stepSize, regParam = regParam, regType = regType, intercept = includeIntercept) logLossValLR1 = evaluateResults(model1, hashValidationData) print ('Validation Logloss for model1:\n\t = {0}' .format(logLossValLR1)) Validation Logloss for model1: = 0.482691122185
次にグリッドサーチを実施してモデル構築します。
numIters = 500 stepSizes = [0.1, 0.5, 1, 3, 5, 7] regParams = [1e-7, 1e-6, 1e-5, 1e-4, 1e-3, 1e-2] regType = 'l2' includeIntercept = True # Initialize variables using values from initial model training bestModel = None bestLogLoss = 1e10 logLoss = np.zeros((len(stepSizes),len(regParams))) for i in xrange(len(stepSizes)): for j in xrange(len(regParams)): model = LogisticRegressionWithSGD.train(data = hashTrainData, iterations = numIters, step = stepSizes[i], regParam = regParams[j], regType = regType, intercept = includeIntercept) logLoss[i, j] = evaluateResults(model, hashValidationData) if (logLoss[i, j] < bestLogLoss): bestModel = model bestStepsize = stepSizes[i] bestParams = regParams[j] bestLogLoss = logLoss[i,j] print ('best parameters:\n\tBest Stepsize = {0:.3f}\n\tBest Rarams = {1:.3f}' .format(bestStepsize, bestParams)) print bestParams,logLoss %matplotlib inline from matplotlib.colors import LinearSegmentedColormap numRows, numCols = len(stepSizes), len(regParams) logLoss = np.array(logLoss) logLoss.shape = (numRows, numCols) fig = plt.figure() ax = plt.subplot(111) ax.set_xticklabels(regParams), ax.set_yticklabels(stepSizes) ax.set_xlabel('Regularization Parameter'), ax.set_ylabel('Step Size') colors = LinearSegmentedColormap.from_list('blue', ['#0022ff', '#000055'], gamma=.2) image = plt.imshow(logLoss,interpolation='nearest', aspect='auto', cmap = colors) pass best parameters: Best Stepsize = 7.000 Best Rarams = 0.000 1e-07 [[ 0.51910013 0.51910015 0.51910029 0.51910175 0.51911634 0.51926454] [ 0.48589729 0.4858974 0.48589847 0.48590921 0.48605802 0.48715278] [ 0.47476165 0.47476184 0.47476375 0.47478289 0.4750353 0.47731296] [ 0.46130496 0.46130542 0.46131004 0.46137622 0.46208485 0.46799094] [ 0.45587263 0.45587339 0.45588094 0.45600577 0.45715016 0.465792 ] [ 0.45268179 0.45268281 0.45270706 0.45286577 0.45438559 0.46488834]]
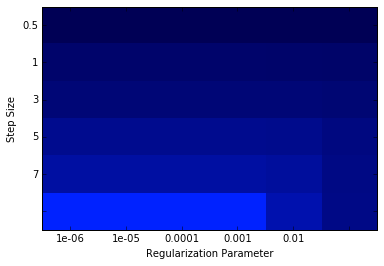
最期に下記の軸によるLoglosによるモデル評価です。
-OHEデータモデル(model1) vs Hushingデータモデル(model2)
-Hushingデータ・デフォルトモデル(model2) vs Hushingデータ・GSモデル(model3)
Loglossでの比較では、次元量を圧縮したHushing後のデータを使っても予測精度が落ちていませんね、面白いです。
logLossTestLR0 = evaluateResults(model0, OHETestData) logLossTestLR1 = evaluateResults(model1, hashTestData) logLossTestLRbest = evaluateResults(bestModel, hashTestData) print ('OHECoding & Hashed Features Test Logloss:\n\tOHEModel = {0:.3f}\n\thashModel = {1:.3f}' .format(logLossTestLR0, logLossTestLR1)) print ('Hashed Features Validation Test Logloss:\n\tBaseModel = {0:.3f}\n\tBestModel = {1:.3f}' .format(logLossTestLR1, logLossTestLRbest)) OHECoding & Hashed Features Test Logloss: OHEModel = 0.490 hashModel = 0.490 Hashed Features Validation Test Logloss: BaseModel = 0.490 BestModel = 0.460
時系列解析① ARモデル
時系列データの解析を二つのデータに対して実施します。
基本的には、RawDataの確認、トレンドと季節性の排除、モデルのフィッティングの順にやっていきます。
データ①simulated data
Rで生成したデータについて分析してみます。
データを作成するコードは下記。
データのプロットと、自己相関関数を併せて出しておきます。
#### Generate time seriese data with a linear trend >time <- 1:200 >data.ar <- arima.sim(model=list(ar=c(0.6, 0.3)), n=200, sd=1) >data <- data.ar + 30 + 0.05 * time >par(mfrow=c(2,1)) >plot(time, data, type="l", main="Raw data plot") >acf(data, main="Sample autocorrelation function")
出てくるデータはこんな感じです。
グラフとコレログラム(Correlogram)から線形トレンドがありそうなので、こいつを取り除きます。
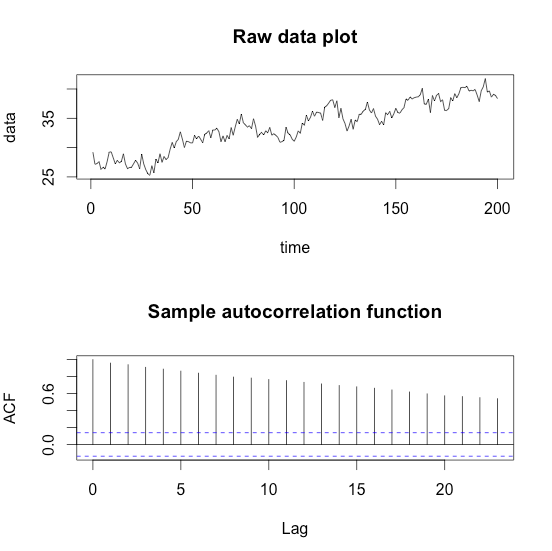
## Remove the trend >linear.model <- lm(data~time) >summary(linear.model) Call: lm(formula = data ~ time) Residuals: Min 1Q Median 3Q Max -3.7143 -1.0238 -0.0246 1.0379 3.7570 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 27.098000 0.207381 130.7 <2e-16 *** time 0.065674 0.001789 36.7 <2e-16 *** >residual.series <- data - linear.model$fitted.values >par(mfrow=c(3,1)) >plot(residual.series, main="Residual series") >acf(residual.series, main="ACF of Residual series") >pacf(residual.series, main="PACF of Residual series")

時系列プロットから定常性が確認でき偏自己相関から、AR(2)が妥当なオーダーだと判断出来ますので、早速モデル化。
## Fit an AR(2) model to the data model.ar <- arima(residual.series, order=c(2,0,0)) par(mfrow=c(3,1)) plot(model.ar$residuals, main="Residual series") acf(model.ar$residuals, main="ACF of Residual series") pacf(model.ar$residuals, main="PACF of Residual series")
ARIMA()関数は残差をプロットしてくれます。
プロットを見る限り、残差に相関はなさそうなのでモデルが妥当だったということでしょう。
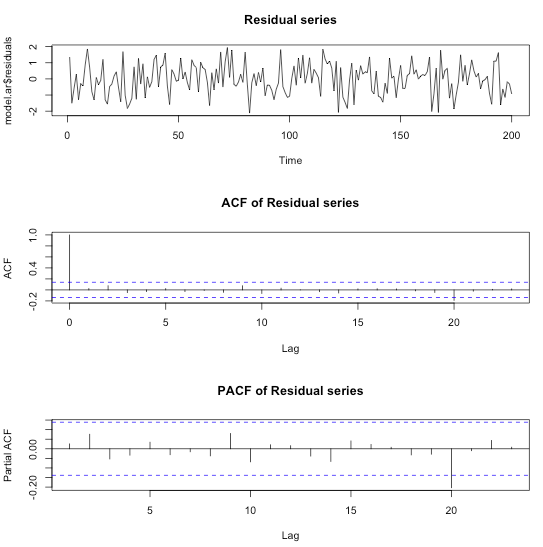
データ②Temperature Data
湖の温度を測ったデータを使っての時系列分析です。
データは私のGitHubに置いてあります。
GitHub:
https://github.com/tkazusa/Sample_code/tree/master/Data
> #Data import > tempeature <- read.csv("temperature.csv", header=TRUE) > t <- 1:nrow(tempeature) > x <- tempeature$Temperature > par(mfrow=c(2,1)) > plot(t,x, type="l", main="Raw data plot") > acf(x,main="Temperature data ACF")
図から、先ほどの例とは異なり季節性が出ていることがわかります。

この季節性を取り除くために、下記のモデルを使います。
> model.season <- lm(x~sin(2*pi*t/365) + cos(2*pi*t/365)) > summary(model.season) Call: lm(formula = x ~ sin(2 * pi * t/365) + cos(2 * pi * t/365)) Residuals: Min 1Q Median 3Q Max -10.3755 -2.1802 -0.0533 2.4349 9.0749 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 6.4263 0.1029 62.47 <2e-16 *** sin(2 * pi * t/365) -2.5477 0.1455 -17.51 <2e-16 *** cos(2 * pi * t/365) -3.7933 0.1455 -26.07 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 3.404 on 1092 degrees of freedom Multiple R-squared: 0.4746, Adjusted R-squared: 0.4736 F-statistic: 493.2 on 2 and 1092 DF, p-value: < 2.2e-16 > residual.series <- x - model.season$fitted.values > par(mfrow=c(3,1)) > plot(residual.series, main="Residual series", type="l") > acf(residual.series, main="ACF of Residual series") > pacf(residual.series, main="PACF of Residual series")

プロットからResidualデータは定常性があり、PACFからAR(1)モデルが妥当だと判断できますので、モデル化します。
>## Fit an AR(1) model > model.ar <- arima(residual.series, order=c(1,0,0)) > model.ar Call: arima(x = residual.series, order = c(1, 0, 0)) Coefficients: ar1 intercept 0.4861 0.0026 s.e. 0.0264 0.1746 sigma^2 estimated as 8.829: log likelihood = -2746.36, aic = 5498.72 > par(mfrow=c(3,1)) > plot(model.ar$residuals, main="Residual series") > acf(model.ar$residuals, main="ACF of Residual series") > pacf(model.ar$residuals, main="PACF of Residual series")
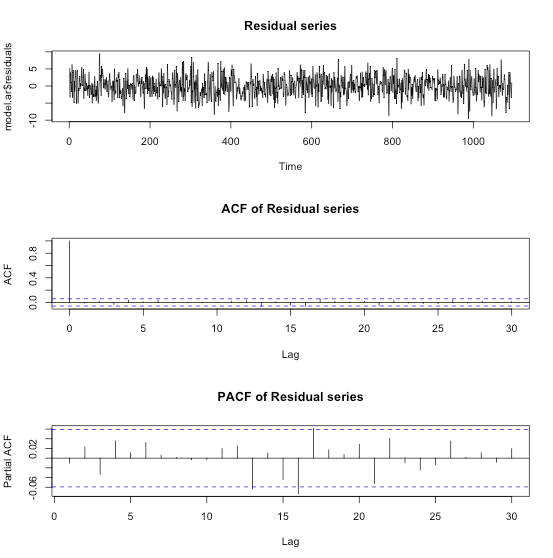
残差プロットやPACFより綺麗にモデル化できていると判断できます。